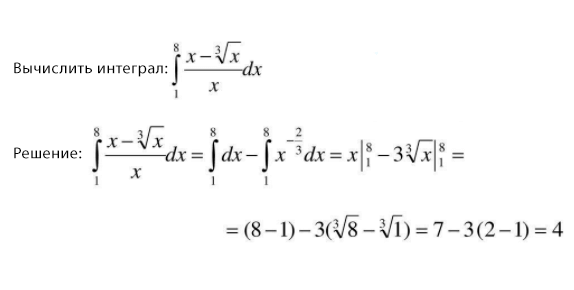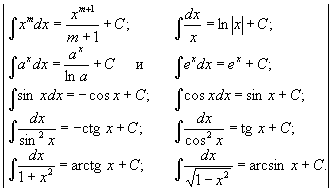Конев В.В. Определенные интегралы
Как произвольная константа интегрирования используется число C , которое можно определить, если известно значение интеграла в какой-нибудь точке. Каждая функция имеет бесконечное число первообразных. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!


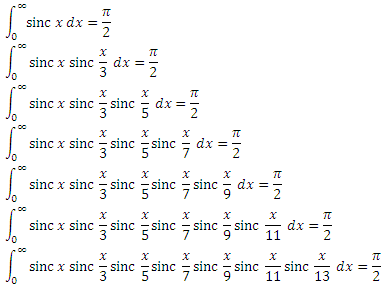
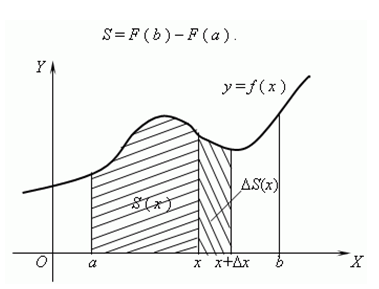

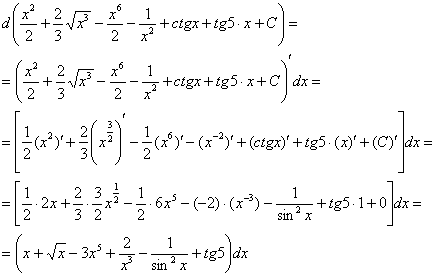
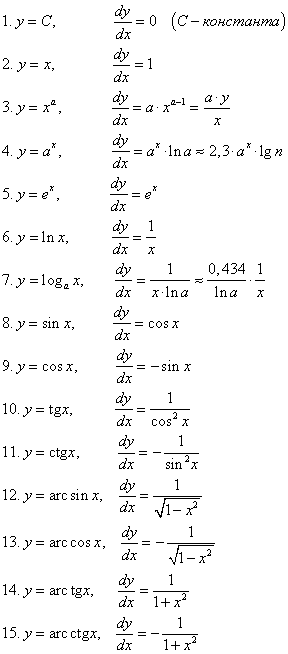

Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых. В зависимости от пространства, на котором задана подынтегральная функция, интеграл может быть двойной , тройной , криволинейный , поверхностный и так далее; также существуют разные подходы к определению интеграла — различают интегралы Римана , Лебега , Стилтьеса и другие [3]. Обозначается это так:.


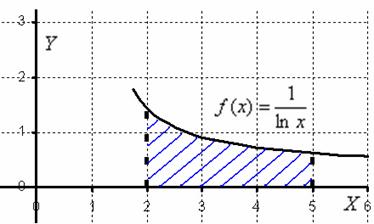

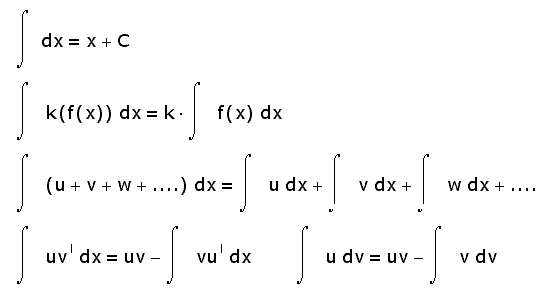
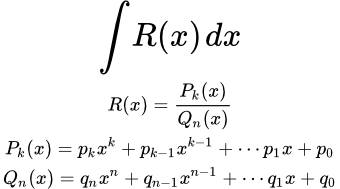
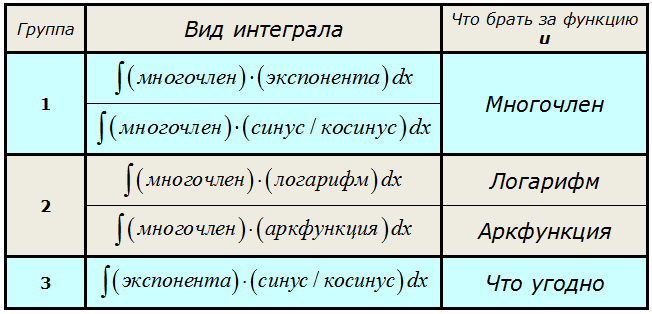

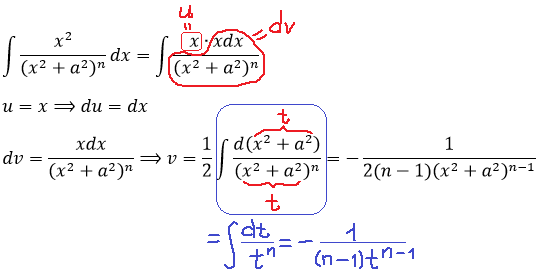
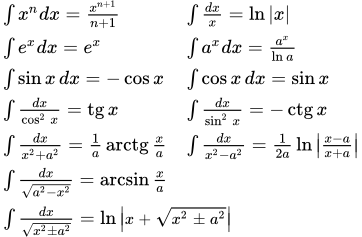



| 432 | Главная Справочник Формулы интегрирования. | |
| 454 | Полная версия материалов. Онлайн обучение по физике и математике у автора этого сайта:. | |
| 440 | Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует. |
Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной. Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью. Данная статья рассматривает применение формулы Ньютона-Лейбница.