Вы точно человек?
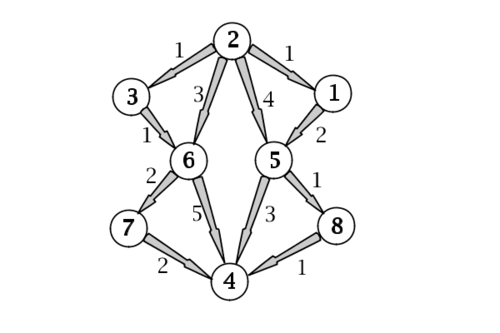
Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре на этой странице. Из определения видно, что соединение графов обладает свойствами коммутативности и ассоциативности.








Теоретическое исследование История возникновения теории графов Разбор задачи «о семи мостах Кёнигсберга» и её решение Основные понятия теории графов Определение понятия «граф» Составляющие графов Виды графов Задачи теории графов и их решение Задача 1. Росчерком пера Задача 2. Задача коммивояжёра Применения теории графов Теория графов в транспортных, коммуникационных и геоинформационных системах Теория графов в медицине Теория графов в биологии Теория графов в химии Графы в физике и технике Графы в информатике Глава II. Генеалогическое древо Приложение 2. Примеры графов в жизни школьника Приложение 3.
- Рабочая программа дисциплины Основы программирования.
- Пользователь приглашает вас присоединиться к открытой игре игре с друзьями. Вход и регистрация.
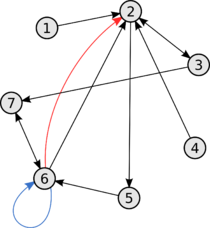
- В теории графов , цикл в графе не является пустым следом , в котором только повторяющиеся вершины являются первой и последней вершины. Направлено цикл в ориентированном графе является непустой направлен след , в котором только повторяющиеся вершины первая и последняя вершина.



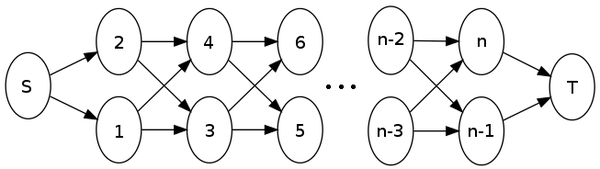



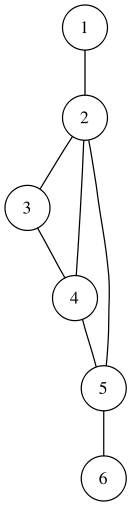


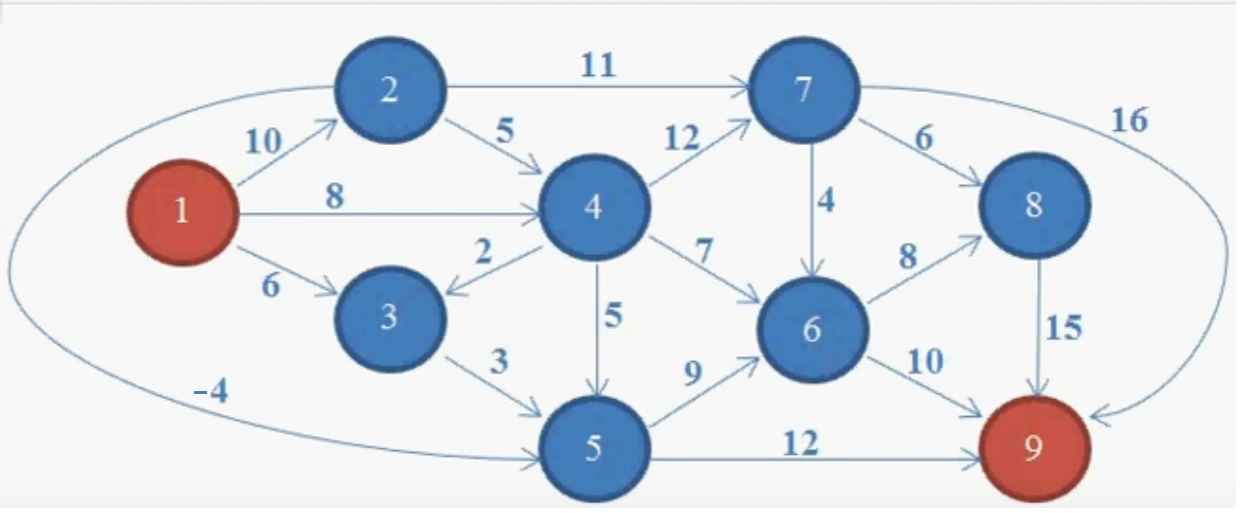
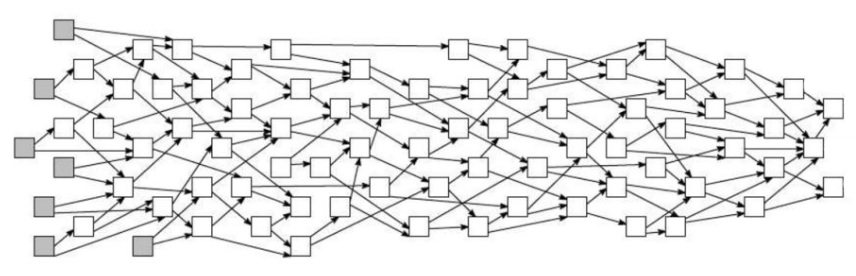
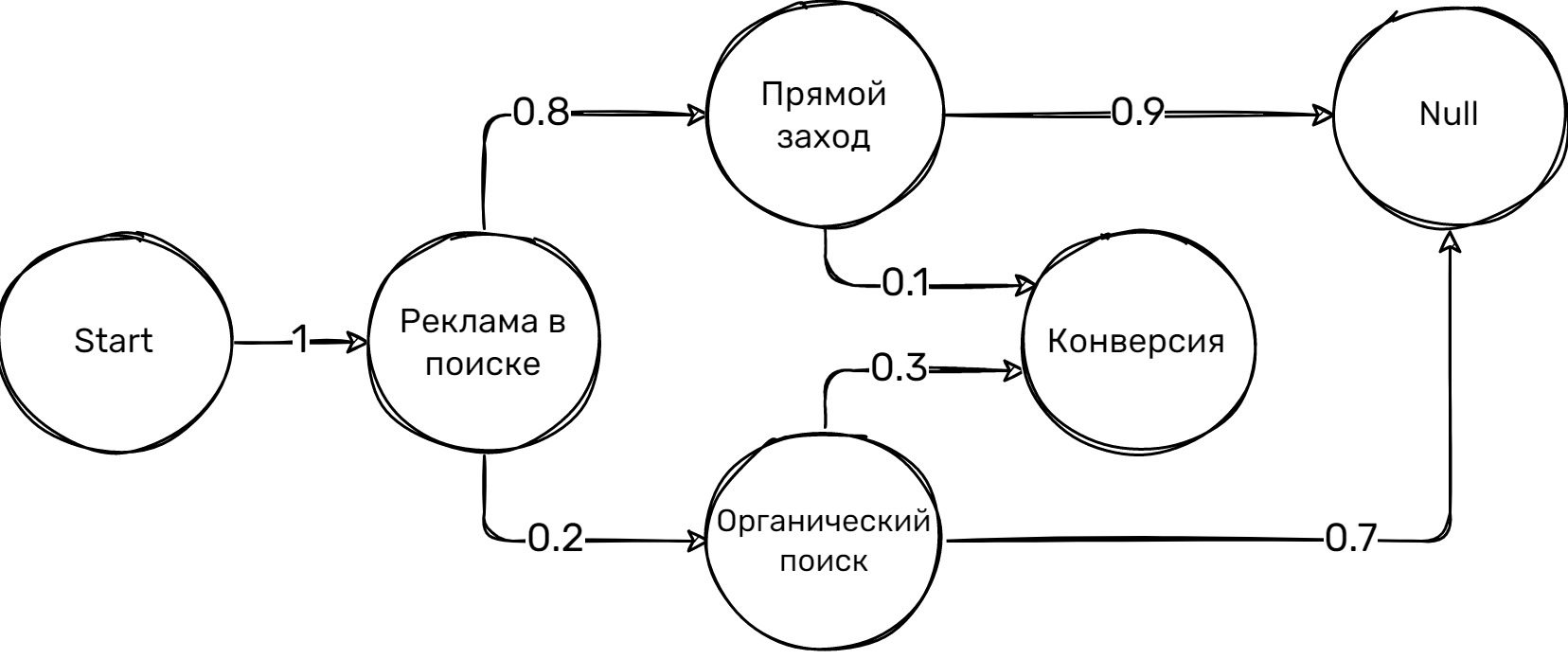
Критический путь графа — путь максимальной длины в ориентированном ациклическом графе. Его длина является минимальной из всех возможных высот у ярусно-параллельной формы данного ациклического графа. При аналитическом задании графа нахождение длины его критического пути как функции внешних параметров задачи является одной из важных задач при распараллеливании алгоритмов. При этом даже в случае, когда алгоритм относится к простому, например, линейному классу, заранее нельзя предугадать, к какому классу функций будет относиться длина критического пути. Скажем, существуют простые примеры, опровергающие гипотезу принадлежности этой функции к классу полиномов. Источник: Википедия.